计算导数
计算导数的方法有:符号导数,有限差分,自动微分等。本文只介绍有限差分和自动微分
有限差分
有限差分就是用有限步长下函数变化率来近似代替导数。
one-side-difference
\[\frac{\partial f}{\partial x_i}(x) \approx \frac{f(x+\epsilon e_i)-f(x)}{\epsilon}\]
利用泰勒公式分析误差,可知误差\(|\delta_{\epsilon}|\leq (L/2)\epsilon\)其中L是\(|\nabla^2 f|\)的上界,这是截断误差,由于计算过程由计算机完成,还存在roundoff-errors,用\(u\)表示(在双精度计算中一般是\(10^{-16}\))假定在计算过程中,相对误差被\(u\)控制,则roundoff误差不超过\(2uL_f/\epsilon\),其中\(L_f\)是f取值上界。那么总误差就是截断误差和roundoff误差的和,可知需要取\(\epsilon=\sqrt{u}\)使误差最小。central-difference
\[\frac{\partial f}{\partial x_i}(x) \approx \frac{f(x+\epsilon e_i)-f(x-\epsilon e_i)}{2\epsilon}\]截断误差为\(O(\epsilon^2)\),考虑到roundoff误差,\(epsilon\)应该取\(u^{2/3}\)
计算稀疏的jacobian
考虑需要计算导数的向量函数\(r:\mathbb{R}^n \rightarrow \mathbb{R}^m\),用有限差分的方法近似为\[J(x)p \approx \frac{r(x+\epsilon p)-r(x)}{\epsilon}\]如果让\(p=\epsilon e_i\),就有\[\frac{\partial r}{\partial x_i}(x)\approx \frac{r(x+\epsilon e_i)-r(x)}{\epsilon}\]要得出近似的jacobian需要计算n个这样的式子,要计算n+1次f的取值,如果jacobian是稀疏的(且我们知道它哪儿为0),进行这么多计算就很浪费。这时有一个技巧,将多个\(e_i\)组合起来,例如计算\(\frac{r(x+\epsilon (e_i+e_j))-r(x)}{\epsilon}\),如果\(\frac{\partial r_1}{\partial x_i}=0\)那就表示上式算出的第一个分量即为\(\frac{\partial r_1}{\partial x_j}\),这样减少了需要计算的点。这些方向的组合方式需要用图染色算法来确定(具体见p179)
自动微分
自动微分将初等函数分解成若干基本初等函数的复合与加减乘除,利用链式法则求出函数对各变量的导数,考虑如下函数
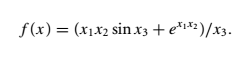
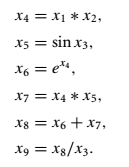
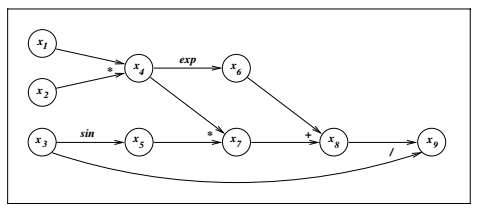
Forward Mode
Forward Mode即从上图中左边开始计算,依次计算每个节点对\(x_1\)的导数,遍历图后得到函数值对\(x_1\)的导数,重复步骤继续得到对其它变量的导数,于是对于\(\mathbb{R}^n \rightarrow \mathbb{R}^m\),这样的步骤需要进行n次。
Reverse Mode
Reverse Mode即从上图右边开始计算,依次计算函数值对每个节点的导数,遍历图后得到函数值对各变量的导数,于是对于\(\mathbb{R}^n \rightarrow \mathbb{R}^m\),这样的步骤需要进行m次
至于计算Hessian什么的也都是差不多了。 具体实现的时候,可以像tensorflow那样,让计算部署过程都被计算图追踪。节点遍历顺序可以用拓扑排序解决。